Mucho
se ha hablado del mecanismo de Higgs para dotar de masa a las
partículas. Pero cuando uno intenta acercarse a este tema se topa con
dos dificultades básicas:
a) El lenguaje y la notación que emplean los físicos en su quehacer diario.b) La impresión de que todo lo relacionado con la física teórica de vanguardia tiene que ser terriblemente complicado desde el punto de vista matemático.
 Sin embargo, soy de la opinión de que hay
algunos temas, evidentemente no todos, que pueden ser explicados a
nivel de instituto con las herramientas matemáticas del bachillerato.
Este ejercicio me parece interesante por varias razones, entre ellas
está que el estudiante pierde el miedo a enfrentarse con conceptos
físicos elevados y por otra parte porque puede ver en acción las cuestiones matemáticas que está estudiando.
Sin embargo, soy de la opinión de que hay
algunos temas, evidentemente no todos, que pueden ser explicados a
nivel de instituto con las herramientas matemáticas del bachillerato.
Este ejercicio me parece interesante por varias razones, entre ellas
está que el estudiante pierde el miedo a enfrentarse con conceptos
físicos elevados y por otra parte porque puede ver en acción las cuestiones matemáticas que está estudiando.
En las dos siguientes entradas espero que
cualquier profesor de física de bachillerato pueda encontrar un
material interesante para echar un rato con sus estudiantes charlando y
trabajando de verdad cuestiones relativas al bosón de Higgs y
de su significado. Que hable de simetrías, de roturas de simetrías y de
generación de masas. Lo más difícil desde el punto de vista
técnico matemático será calcular unos mínimos de una función de una
variable (que resultará ser polinómica).
El punto clave está en presentar el tema
explicando la notación, perdiéndole el respeto y jugando con las
fórmulas sin ningún tipo de complejo.
Espero que esta entrada sea del gusto de algún profesor y que, si así lo considera oportuno, la use en sus clases cuando guste.
Tengo que decir que yo no he dado clases a estos niveles así que sed benevolentes conmigo porque la intención es buena.
¿Lagran… qué?
Si tuviera que decir cuál es el elemento fundamental en física de partículas diría que es el langrangiano. (Ya empezamos con las palabrejas)
De un lagrangiano se obtienen las
ecuaciones físicas de los sistemas, cómo evolucionan con el tiempo, como
interactúan, en definitiva, toda la información relevante.
Nota para profesores: Si quieres refrescar eso del lagrangiano y su utilidad tal vez te resulte útil esta entrada, Mecánica Lagrangiana y esta otra Ejercicio de mecánica lagrangiana.
La lagrangiana de un sistema (a veces diré lagrangiano y otras lagrangiana) no es más que una combinación de dos términos:
Lagrangiana = Energía Cinética – Energía Potencial
Así de fácil. Todo lo que tenemos que
hacer es ver qué es la energía cinética de nuestro sistema, energía
debida a su movimiento de traslación, y cuál es la energía potencial del
mismo. Las restamos y obtenemos un objeto matemático que contiene toda
la información relevante para establecer el comportamiento dinámico del
sistema bajo estudio.
Nota
para profesores: En las entradas que he indicado más arriba hay
ejemplos claros de cómo formular una lagrangiana y ver cómo se obtienen
los resultados que obtendríamos con mecánica de Newton para sistemas
mecánicos simples. Es una bonita forma de decirle a los estudiantes que
hay vida más allá de Newton y que el estudio de la energía de un sistema
siempre es algo bueno y beneficioso.
La lagrangiana del Higgs
Si abrimos cualquier libro o artículo
científico de física de partículas o de teoría cuántica de campos que
traten sobre el Higgs nos encontraremos con una lagrangiana de este
tipo:
Antes de seguir es bueno hacer esta simple manipulación que consiste en sacar un signo menos factor común:
 Nota
para profesores: Los términos cinéticos de las lagrangianas siempre
van con las derivadas de los campos respecto a las coordenadas
espaciotemporales, los términos cuadráticos con
Nota
para profesores: Los términos cinéticos de las lagrangianas siempre
van con las derivadas de los campos respecto a las coordenadas
espaciotemporales, los términos cuadráticos con
Es hora de presentar las letras esas que aparecen por ahí en esa fórmula del lagrangiano del Higgs:
1.- El campo de Higgs viene representado por  .
Este es el actor principal y a todos los efectos representa la variable
de nuestro problema. Hasta que se indique lo contrario
.
Este es el actor principal y a todos los efectos representa la variable
de nuestro problema. Hasta que se indique lo contrario  es una variable real.
es una variable real.
2.- Los amigos 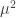 y
y  son parámetros reales. Por ahora su signo no está definido pero nos pararemos a discutir ese aspecto en breve.
son parámetros reales. Por ahora su signo no está definido pero nos pararemos a discutir ese aspecto en breve.
3.- El término relativo a la energía
cinética del campo, porque los campos se pueden propagar, es el
contenido en la parte de la lagrangiana correspondiente a  . Este término podemos olvidarlo ya que lo importante pasa en la energía potencial.
. Este término podemos olvidarlo ya que lo importante pasa en la energía potencial.
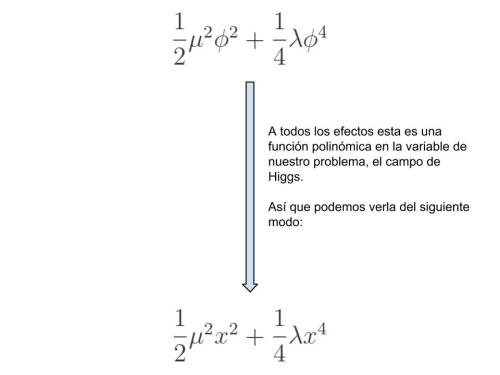
4.- La energía potencial del campo, la actriz principal de esta historia, corresponde a:  . A todos los efectos entenderemos esa expresión como si el campo fuera una variable, digamos la variable x.
. A todos los efectos entenderemos esa expresión como si el campo fuera una variable, digamos la variable x.
Todo lo que vamos a hacer, por ahora, es buscar mínimos de esta función de la energía potencial.
Pero antes de eso…Qué bonita es la simetría
Volvamos a mirar la lagrangiana completa del Higgs una vez más.
Tal vez tengamos que expandirla un poco más aún:
A este nivel entendemos que una simetría
se presenta cuando hacemos una transformación matemática a los objetos
fundamentales de nuestro problema, en nuestro caso el campo de Higgs  , y la lagrangiana no sufre ningún cambio, se queda tal cual.
, y la lagrangiana no sufre ningún cambio, se queda tal cual.
Dado que como hemos dicho la lagrangiana
contiene toda la información acerca de la física del problema, sobre la
propagación del campo, sobre su energía, sobre sus interacciones, etc,
si esta no se entera cuando hacemos una transformación sobre el campo,
(queda invariante), la física no sentirá nada con ese cambio.
Pero lo mejor es verlo en acción.
Supongamos que nos da el arrebato de cambiar de signo el campo, es decir, transformamos el campo del siguiente modo:
¿Qué le pasa a nuestra lagrangiana cuando cambiamos de signo el campo?
 Es decir, la transformación elegida es una simetría ya que deja invariante al lagrangiano de nuestra teoría.
Es decir, la transformación elegida es una simetría ya que deja invariante al lagrangiano de nuestra teoría.
Nota para profesores: En este punto se pueden refrescar las ideas sobre funciones pares e impares.
Jugando con la parte potencial
Nos vamos a centrar ahora en la parte potencial, es decir, en la función:
Para poder trabajar con ella tenemos que darle valores a los parámetros 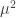 y
y  . Supondremos que
. Supondremos que  es un parámetro real y positivo y, para simplificarnos la vida, podemos elegir que valga 1.
es un parámetro real y positivo y, para simplificarnos la vida, podemos elegir que valga 1.
Con el 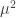 hay más sutilezas. Este parámetro es importante en física por la siguiente razón:
hay más sutilezas. Este parámetro es importante en física por la siguiente razón:
 Por lo tanto, el parámetro
Por lo tanto, el parámetro
Nota
para profesores: El hecho de que el parámetro en el término cuadrático
en el campo de una lagrangiana corresponda a una masa al cuadrado tiene
que ver con varios motivos. El primero es porque dimensionalmente tiene
que ser así, el 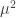 ha de tener dimensiones de masa al cuadrado. En segundo lugar, y más
importante, es porque en un tratamiento cuántico relativista ese término
indica en cierto modo la forma que tiene el campo al interactuar con el
vacío lo que nos da idea de su inercia y por lo tanto de su masa. En
la expresión que estamos manejando hemos eludido poner constantes
físicas tales como la velocidad de la luz en el vacío o la constante de
Planck y por eso no es inmediato ver la homogeneidad dimensional de la
expresión.
ha de tener dimensiones de masa al cuadrado. En segundo lugar, y más
importante, es porque en un tratamiento cuántico relativista ese término
indica en cierto modo la forma que tiene el campo al interactuar con el
vacío lo que nos da idea de su inercia y por lo tanto de su masa. En
la expresión que estamos manejando hemos eludido poner constantes
físicas tales como la velocidad de la luz en el vacío o la constante de
Planck y por eso no es inmediato ver la homogeneidad dimensional de la
expresión.
Como es
conocido los campos cuánticos tienen partículas asociadas, dichas
partículas tienen una masa definida. Podríamos tener la tentación de
pensar que la masa de dichas partículas es simplemente la raíz cuadrada
de 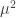 .
Sin embargo esa primera idea no funciona, para determinar la masa
física del campo (o de sus partículas asociadas) hay que trabajar un
poco más el tema y es en lo que estamos.
.
Sin embargo esa primera idea no funciona, para determinar la masa
física del campo (o de sus partículas asociadas) hay que trabajar un
poco más el tema y es en lo que estamos.
Sin embargo, por ahora vamos a decir que el parámetro 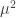 nos da una idea de la resistencia que presenta el campo a cambiar de valor, algo así como un coeficiente de rozamiento.
nos da una idea de la resistencia que presenta el campo a cambiar de valor, algo así como un coeficiente de rozamiento.
Vamos a estudiar los dos casos posibles del signo del parámetro 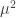 .
.
a) Cuando el parámetro 
Sin pérdida de generalidad elegimos que  y, como hemos dicho,
y, como hemos dicho,  . Por lo tanto la función potencial del campo toma la forma:
. Por lo tanto la función potencial del campo toma la forma:
La gráfica de esta función es:
1. Para empezar hacemos la derivada de la función respecto de su variable y la igualamos a cero.
La derivada de la función queda:
Igualando a cero obtenemos:
Esto nos deja con dos posibles soluciones:
y
Por lo tanto, el punto donde es posible que esté el mínimo corresponde al valor 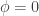 , sustituyendo ese valor en la función
, sustituyendo ese valor en la función 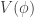 obtenemos:
obtenemos:
Así que el punto extremo es el (0,0).
2.- Recurrimos al criterio de la segunda derivada para determinar si estamos ante un máximo o un mínimo:
El cálculo de la segunda derivada de la función queda:
Sustituyendo el valor crítico de la variable 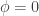 en la segunda derivada:
en la segunda derivada:
Dado que 4>0, resulta que en el punto (0,0) tenemos un mínimo de la función.
b) Caso del parámetro 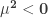
Sin pérdida de generalidad elegimos que 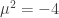 y, como hemos dicho,
y, como hemos dicho,  . Por lo tanto la función potencial del campo toma la forma:
. Por lo tanto la función potencial del campo toma la forma:
Nota para profesores: En este caso lo que tenemos entre manos es un  complejo, de hecho imaginario puro. Eso dificulta la interpretación del
mismo como una masa. Desde el punto de vista físico formal nos estamos
enfrentando a la aparición de un taquión en nuestra teoría. Dado que
eso no es aceptable la propia teoría tiene que tener las herramientas
necesarias como para estabilizar esta situación. Como veremos este es
el caso. Este hecho es el que hace preferible interpretar el
complejo, de hecho imaginario puro. Eso dificulta la interpretación del
mismo como una masa. Desde el punto de vista físico formal nos estamos
enfrentando a la aparición de un taquión en nuestra teoría. Dado que
eso no es aceptable la propia teoría tiene que tener las herramientas
necesarias como para estabilizar esta situación. Como veremos este es
el caso. Este hecho es el que hace preferible interpretar el 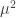 como una medida de la resistencia al cambio de valor del campo en vez
de una masa ya que podremos llamarlo masa propiamente dicha cuando el
parámetro que acompañe al término cuadrático del campo en la lagrangiana
sea positivo. De todas formas este parámetro siempre aparecerá elevado
al cuadrado. Este es uno de los puntos esenciales de toda la discusión
acerca del mecanismo de Higgs de generación de masa de otros campos. Se
puede aprovechar esta circunstancia para hablar un poco de números
complejos y sus particularidades.
como una medida de la resistencia al cambio de valor del campo en vez
de una masa ya que podremos llamarlo masa propiamente dicha cuando el
parámetro que acompañe al término cuadrático del campo en la lagrangiana
sea positivo. De todas formas este parámetro siempre aparecerá elevado
al cuadrado. Este es uno de los puntos esenciales de toda la discusión
acerca del mecanismo de Higgs de generación de masa de otros campos. Se
puede aprovechar esta circunstancia para hablar un poco de números
complejos y sus particularidades.
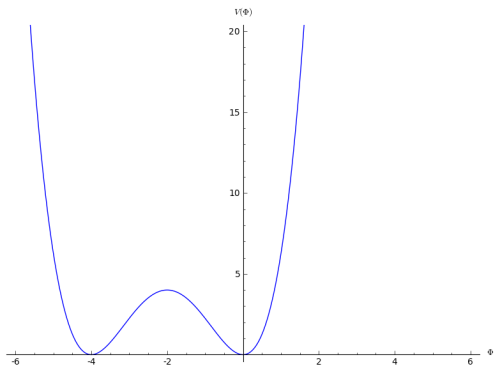
La gráfica de esta función es:
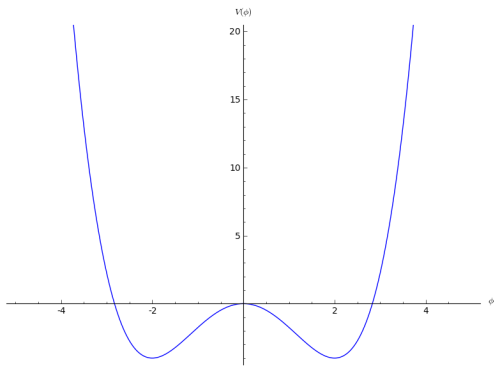 Dado
que esta es una situación de interés físico en lo que sigue
trabajaremos en general, sin introducir los valores del parámetro hasta
el resultado final.
Dado
que esta es una situación de interés físico en lo que sigue
trabajaremos en general, sin introducir los valores del parámetro hasta
el resultado final.
Así trabajaremos con la función:
y sustituiremos los valores de los parámetros al final del cálculo.
Calculemos sus mínimos
1.- Calculamos la primera derivada de la función respecto al campo y la igualamos a cero:
La derivada queda como sigue:
Igualamos a cero y resolvemos:
De aquí obtenemos tres posibles soluciones:
Notemos que la raíz cuadrada está bien definida ya que si 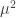 es negativo,
es negativo,  es positivo y el resultado de la raíz es un número real.
es positivo y el resultado de la raíz es un número real.
Por comodidad, llamaremos:
2.- Recurrimos al criterio de la segunda derivada para catalogar los puntos críticos dados por las anteriores expresiones.
Así para 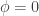 tendremos que la segunda derivada vale
tendremos que la segunda derivada vale 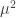 que es un valor negativo y por lo tanto indica que en el punto (0,0) tenemos un máximo local de la función.
que es un valor negativo y por lo tanto indica que en el punto (0,0) tenemos un máximo local de la función.
Para el valor, 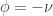 , la segunda derivada vale
, la segunda derivada vale  que es un valor positivo y obtenemos que en el correspondiente punto (
que es un valor positivo y obtenemos que en el correspondiente punto (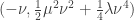 ) tenemos un mínimo.
) tenemos un mínimo.
Veremos que ocurre lo mismo al sustituir el valor 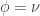 en la segunda derivada, teniendo un mínimo en el punto correspondiente (
en la segunda derivada, teniendo un mínimo en el punto correspondiente ( ).
).
Si sustituímos los valores asignados al principio, 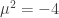 y
y  , los valores del campo para los que tenemos los mínimos son:
, los valores del campo para los que tenemos los mínimos son:
lo que se podía apreciar desde el principio en la figura.
Interpretando a 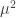
Ya hemos hecho el estudio de los posibles
mínimos de los potenciales en función en los dos posibles casos del
signo del parámetro 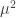 .
En esta sección lo que vamos a plantearnos es su significado y el
estudio de las gráficas que pululan por ahí en los textos divulgativos
sobre el mecanismo de Higgs.
.
En esta sección lo que vamos a plantearnos es su significado y el
estudio de las gráficas que pululan por ahí en los textos divulgativos
sobre el mecanismo de Higgs.
Caso de parámetro 
La gráfica del potencial, como hemos dicho, tiene la siguiente forma (la gráfica está hecha tomando  y
y  ):
):
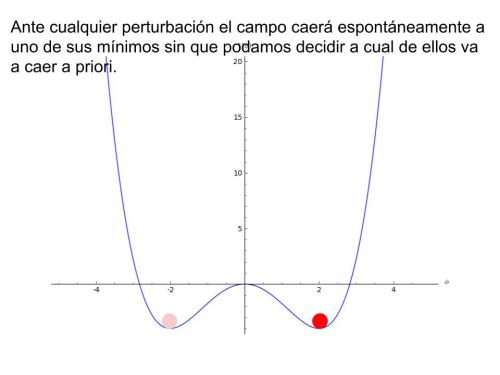
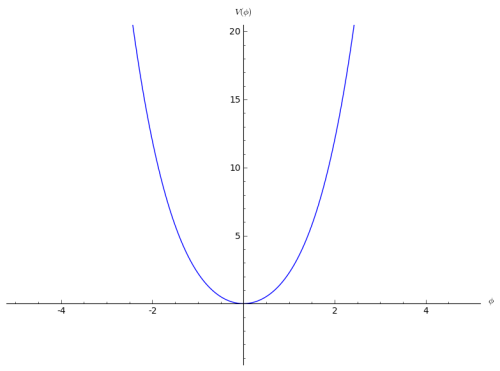 En divulgación se suele hacer uso de una “bolita” para representar al campo, y es usual ver cosas así:
En divulgación se suele hacer uso de una “bolita” para representar al campo, y es usual ver cosas así: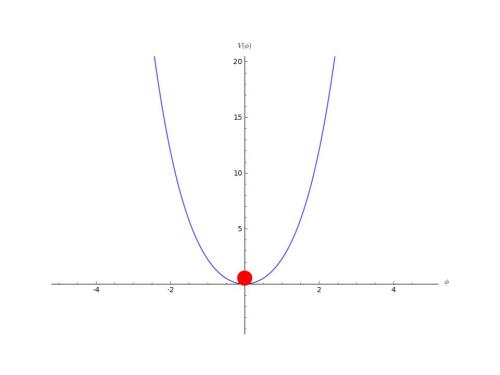 ¿Qué
significa esto? Pues evidentemente no significa que el campo sea como
una bolita que rueda. Aunque el símil es adecuado, por las razones que
vamos a exponer a continuación, puede confundir más que ayudar.
¿Qué
significa esto? Pues evidentemente no significa que el campo sea como
una bolita que rueda. Aunque el símil es adecuado, por las razones que
vamos a exponer a continuación, puede confundir más que ayudar.
Lo que quiere decir esa imagen es que el
campo está en el valor que le corresponde al mínimo del potencial, es
decir, tiene el valor 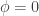 . Si está en otra posición pues indicará el valor del campo y su correspondiente energía:
. Si está en otra posición pues indicará el valor del campo y su correspondiente energía:
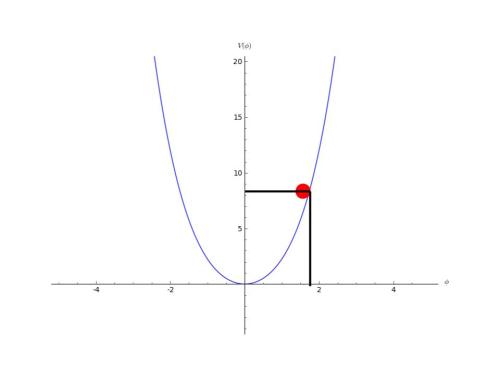 La bolita por lo tanto SOLO nos indica el valor que tiene el campo y la energía que tiene en ese valor.
La bolita por lo tanto SOLO nos indica el valor que tiene el campo y la energía que tiene en ese valor.
La analogía con la bolita puede ser útil si entendemos el parámetro 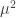 como la “resistencia” del campo a cambiar su valor. Así pues, si
dejamos al campo evolucionar libremente ocupará su mínimo de potencial,
si intentamos moverlo de ahí, que el campo cambie su valor, (estaremos
intentando aumentar su energía), encontraremos resistencia y se
“empeñará” en permanecer en su mínimo. Esta es una situación estable.
como la “resistencia” del campo a cambiar su valor. Así pues, si
dejamos al campo evolucionar libremente ocupará su mínimo de potencial,
si intentamos moverlo de ahí, que el campo cambie su valor, (estaremos
intentando aumentar su energía), encontraremos resistencia y se
“empeñará” en permanecer en su mínimo. Esta es una situación estable.
Este caso no presenta mucho interés.
Caso de parámetro 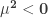
En este caso vamos a encontrar
situaciones más interesantes. Si nos fijamos en la forma de la función
del potencial (calculada con 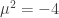 y
y  ) y consideramos que el campo está en su valor nulo:
) y consideramos que el campo está en su valor nulo:
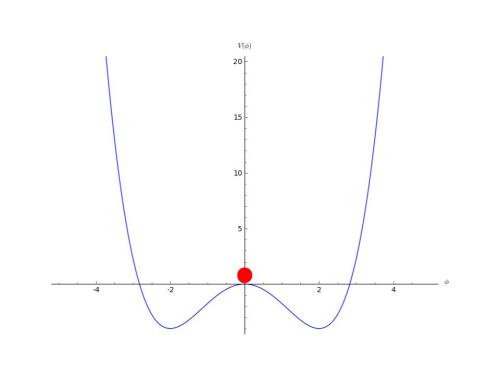 Lo
que tenemos que pensar es que la resistencia que presenta al cambio de
esa posición es negativa. Eso se traduce en que cualquier
desplazamiento para alejarse de ese valor y caer a uno de sus mínimos se
ve favorecido. Esto lo que representa es una situación inestable.
Lo
que tenemos que pensar es que la resistencia que presenta al cambio de
esa posición es negativa. Eso se traduce en que cualquier
desplazamiento para alejarse de ese valor y caer a uno de sus mínimos se
ve favorecido. Esto lo que representa es una situación inestable.
Nota
para profesores: Este tipo de razonamientos son un tanto heurísticos
pero capturan en gran medida los conceptos que podríamos extraer de un
minucioso análisis de las ecuaciones implicadas en esta cadena de
argumentos. Lo que hemos expuesto en las líneas anteriores es
perfectamente válido aunque no totalmente correcto desde el punto de
vista formal. Evidentemente aquí estamos trabajando con los valores que
toma un campo distribuido a su vez por todo el espacio y estamos
forzando la analogía al considerarlo como una bolita que se mueve por un
terreno con subidas y bajadas.
Este caso con el parámetro 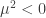 es el que corresponde a un sistema en el que se puede dar el mecanismo
de Higgs. La razón la veremos en breve, el mecanismo de Higgs se basa en
una rotura de simetría y vamos a estudiar que ese es el caso cuando el
campo cae a uno de sus vacíos.
es el que corresponde a un sistema en el que se puede dar el mecanismo
de Higgs. La razón la veremos en breve, el mecanismo de Higgs se basa en
una rotura de simetría y vamos a estudiar que ese es el caso cuando el
campo cae a uno de sus vacíos.
A partir de ahora nos centraremos en este caso.
No es bueno trabajar con parámetros con dimensiones de masa imaginarios
Hemos elegido que nuestro campo tenga la energía potencial correspondiente al caso 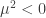 y hemos dicho que el parámetro tiene las dimensiones de una masa al cuadrado resulta que
y hemos dicho que el parámetro tiene las dimensiones de una masa al cuadrado resulta que  tiene dimensiones de masa pero es un número imaginario puro, de la forma
tiene dimensiones de masa pero es un número imaginario puro, de la forma  siendo
siendo  un número real. Sería interesante poder librarnos de este
contratiempo, las masas tienen que ser reales porque son cantidades
observables (medibles). Afortunadamente hay un procedimiento para
librarse de este pequeño contratiempo.
un número real. Sería interesante poder librarnos de este
contratiempo, las masas tienen que ser reales porque son cantidades
observables (medibles). Afortunadamente hay un procedimiento para
librarse de este pequeño contratiempo.
El truco es extremadamente simple, diremos que nuestro campo  , en realidad es un campo
, en realidad es un campo  al que se le ha sumado una constante de valor
al que se le ha sumado una constante de valor  (el valor del campo
(el valor del campo  que sitúa los mínimos del potencial). Es decir:
que sitúa los mínimos del potencial). Es decir:
¿Y eso no lo cambia todo? La respuesta es no.
Lo único que hacemos considerando ese cambio es que nuestro campo inicial  en realidad no es más que un campo
en realidad no es más que un campo  desplazado un factor
desplazado un factor 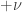 . Pero la física no puede depender de redefinir un campo por una constante.
. Pero la física no puede depender de redefinir un campo por una constante.
Nota para profesores: Esta redefinición, pasar de  a
a  solo involucra a una constante. Esto no es problemático y la física
descrita no se vería afectada. Hay varias razones para ello, lo primero
es que las ecuaciones de evolución dinámica de los sistemas involucran
derivadas de los campos (por ejemplo las ondas electromagnéticas) y por
lo tanto, sumar o restar constantes es irrelevante para las ecuaciones
de ondas, las de movimiento de la mecánica, etc. Por otra parte, es un
buen momento para recordar que hay cosas que no están definidas de
manera absoluta, por ejemplo la energía potencial, y que podemos poner
el origen del potencial gravitatorio (por poner un ejemplo) en el suelo,
en lo alto de una torre o en el infinito. La elección depende del
problema pero con cualquier origen se obtienen los mismos resultados
físicos. Si lo vemos desde el punto de vista de la mecánica
lagrangiana, pues alterar de esta forma el campo puede que nos revele un
mejor entendimiento de la física que esconde. Lo más grave que va a
pasar es una modificación del potencial, pero eso, cuando se introdujera
la cuántica solo nos diría que el campo que estamos tratando puede
interactuar de más formas de las que esperábamos en un principio.
solo involucra a una constante. Esto no es problemático y la física
descrita no se vería afectada. Hay varias razones para ello, lo primero
es que las ecuaciones de evolución dinámica de los sistemas involucran
derivadas de los campos (por ejemplo las ondas electromagnéticas) y por
lo tanto, sumar o restar constantes es irrelevante para las ecuaciones
de ondas, las de movimiento de la mecánica, etc. Por otra parte, es un
buen momento para recordar que hay cosas que no están definidas de
manera absoluta, por ejemplo la energía potencial, y que podemos poner
el origen del potencial gravitatorio (por poner un ejemplo) en el suelo,
en lo alto de una torre o en el infinito. La elección depende del
problema pero con cualquier origen se obtienen los mismos resultados
físicos. Si lo vemos desde el punto de vista de la mecánica
lagrangiana, pues alterar de esta forma el campo puede que nos revele un
mejor entendimiento de la física que esconde. Lo más grave que va a
pasar es una modificación del potencial, pero eso, cuando se introdujera
la cuántica solo nos diría que el campo que estamos tratando puede
interactuar de más formas de las que esperábamos en un principio.
Aceptando el hecho de que meter en juego
una constante no modifica la física el siguiente paso es introducir en
nuestra lagrangiana inicial el cambio propuesto.
Si partimos de la lagrangiana:
Al introducir el cambio  tendríamos que ver qué resulta al desarrollar la siguiente expresión:
tendríamos que ver qué resulta al desarrollar la siguiente expresión:
Después de unas cuantas líneas de calculitos* (Los cálculos detallados están al final de la entrada) obtenemos:
¿Identificáis el término de masas? Era
fácil, solo había que mirar la lagrangiana y buscar el término que lleva
el campo al cuadrado, en este caso el término que va con  . Es directo ver que ese término es:
. Es directo ver que ese término es:
Como hemos dicho cuando un físico ve eso
lo asocia a un término de masa. Pero falta un detalle, los términos de
masa tienen siempre esta estructura:
En nuestro caso tendríamos  , así que igualando coeficientes:
, así que igualando coeficientes:
Despejando la masa nos queda:
Y recordando que  podemos ver que el término de masa no es más que:
podemos ver que el término de masa no es más que:
¡Maravilloso! Porque este término ahora ¡¡¡SÍ ES POSITIVO!!! (porque nuestro 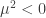 )
)
¿Qué efecto ha tenido todo esto en la gráfica del potencial?
Pues veámoslo, la función del potencial, ahora para el campo  es:
es:
Y su gráfica es:
Con el desplazamiento del campo inicial  ahora trabajamos con el campo
ahora trabajamos con el campo  . Hemos obtenido que la energía de este nuevo campo se ha desplazado (
. Hemos obtenido que la energía de este nuevo campo se ha desplazado ( unidades hacia la izquierda) y uno de los mínimos correponde a su estado de valor
unidades hacia la izquierda) y uno de los mínimos correponde a su estado de valor 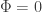 .
.
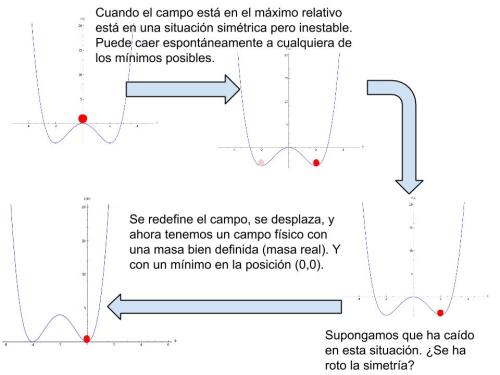
Un resumen de todo esto lo podemos ver en la siguiente imagen:
Con esto terminamos esta primera
entrada. En la siguiente hablaremos del significado físico de todo esto
y de su generalización a casos más realistas. Espero que que os haya
resultado interesante.
Todas las gráficas de esta entrada han sido hechas con Sage: Sagemath.org.
Por supuesto, estaré encantado de conocer vuestra opinión, críticas, dudas o sugerencias de mejora.
Nos seguimos leyendo…
Tomado de: http://cuentos-cuanticos.com/2014/06/26/el-mecanismo-de-higgs-para-estudiantes-de-bachillerat-i/





No hay comentarios:
Publicar un comentario